Shear Strain | Shear Deformation | General Shear Strain | Shear Stress | Complementary Shear Stress | Shear Modulus | Elastic Shear Strain Energy Density


| 3.2 Shear Stress and Strain Shear Strain | Shear Deformation | General Shear Strain | Shear Stress | Complementary Shear Stress | Shear Modulus | Elastic Shear Strain Energy Density |


|
|
» Shear Deformation
|
|
» General Shear Strain
|
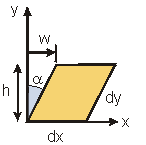 |
|
|
||
|
» Shear Stress
|
The cross-sectional area of a |
|
| SHEAR YIELD STRENGTH: the value of shear stress when the shear stress-shear strain relationship is no longer linear. | ||
|
» Complementary Shear Stress
|
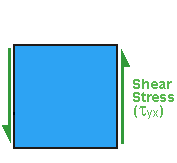
Click Here to see the Complementary Shear Stress |
|
» Shear Modulus
For for most metals, n ~ 1/3, which means the G can be approximated:
| |||||||||||
| » Elastic Shear Strain Energy Density
The maximum value of the elastic strain energy is the |SHEAR RESILIENCE. It occurs when the stress in the stress reaches the shear yield strength:
|

|



|